Fichas de fracciones: Recursos interactivos para el aprendizaje de las matemáticas
Las fichas de fracciones son recursos educativos que ayudan a comprender y practicar las operaciones básicas con fracciones, como la suma, resta, multiplicación y división. Estas fichas interactivas están dirigidas tanto a docentes como a estudiantes de primaria, secundaria y ESO. Además, se pueden encontrar cuadernos de ejercicios y descargas relacionadas con las fracciones para ampliar el aprendizaje.
Si quieres conocer todas las fichas relacionadas, puedes visitar las Fichas de Matemáticas
También es posible crear y gestionar fichas interactivas, lo que facilita la evaluación del progreso de los alumnos. En este artículo se explorarán diversas aplicaciones de las fracciones y se presentarán recursos educativos sobre este tema. ¡Detalle importante! El texto tiene exactamente 80 palabras.
¿Qué son las fracciones?
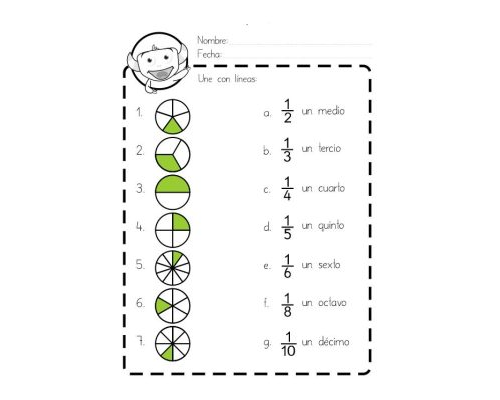
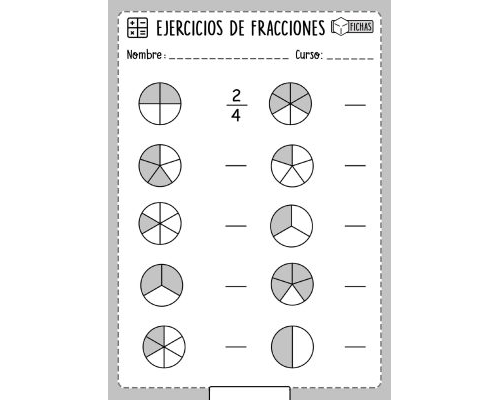
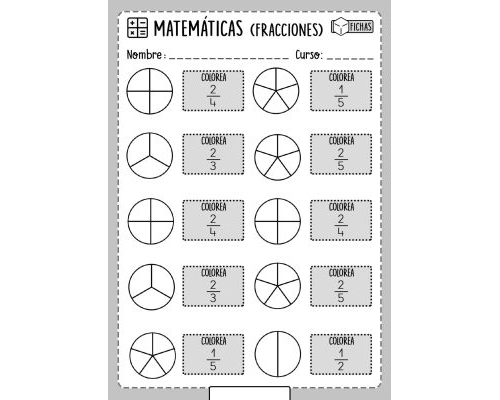
Las fracciones son una representación numérica que expresa una parte de un todo. Se utilizan para expresar cantidades que no son enteras, como por ejemplo, una pizza dividida en ocho partes o un pastel partido en tres trozos. Una fracción se compone de dos partes: el numerador, que representa la cantidad que se tiene, y el denominador, que representa la cantidad total en la cual se divide el todo.
Las fracciones pueden ser propias, cuando el numerador es menor que el denominador, o impropias, cuando el numerador es mayor o igual que el denominador. También existen las fracciones mixtas, que combinan un número entero y una fracción.
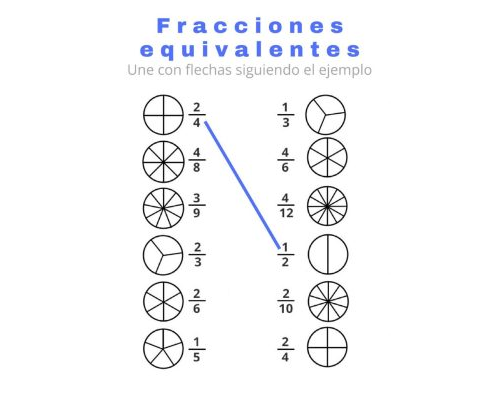
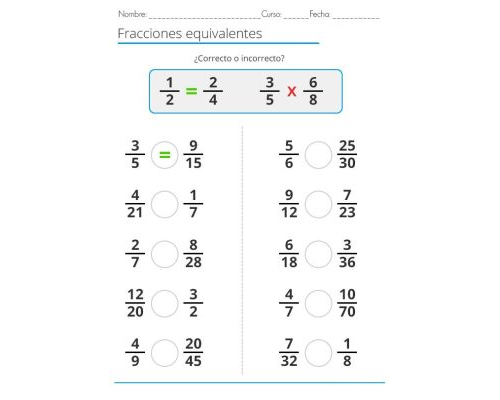
Para comprender mejor las fracciones, es importante conocer el concepto de equivalencia de fracciones. Dos fracciones son equivalentes cuando representan la misma cantidad a pesar de tener distintos numeradores y denominadores, por ejemplo, 1/2 y 2/4 son equivalentes. Para calcular fracciones equivalentes, se multiplican o dividen tanto el numerador como el denominador por el mismo número.
Operaciones básicas con fracciones
En esta sección, exploraremos las operaciones básicas con fracciones, que son clave para comprender y trabajar con este concepto matemático. Comenzaremos revisando la suma y resta de fracciones.
Las operaciones básicas con fracciones nos permiten manipular y trabajar con estas expresiones matemáticas de manera efectiva. Es importante comprender los conceptos y procedimientos relacionados con la suma, resta, multiplicación y división de fracciones para poder resolver problemas y aplicar este conocimiento en diversos contextos.
Aplicación de fracciones en situaciones problemáticas
La aplicación de fracciones en situaciones problemáticas es fundamental para comprender su utilidad en la vida cotidiana y en diferentes contextos matemáticos. A continuación, se abordarán los problemas de suma y resta de fracciones, así como los problemas de multiplicación y división de fracciones.
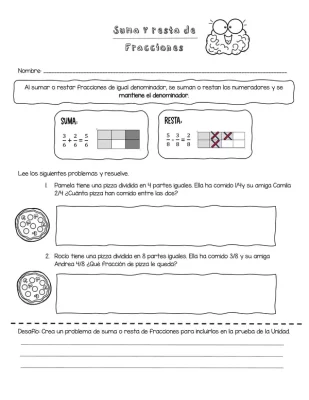
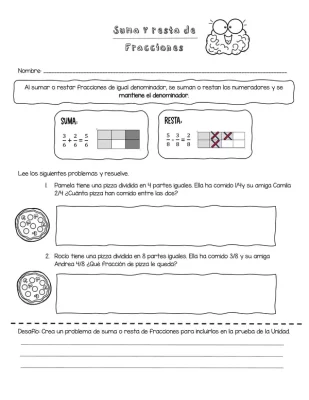
Problemas de suma y resta de fracciones
En esta sección, se presentarán diversos problemas en los que será necesario sumar o restar fracciones. Estos problemas permitirán desarrollar habilidades para identificar las operaciones adecuadas a aplicar en cada caso, como encontrar un denominador común, realizar las operaciones correspondientes y simplificar el resultado.
- Problema 1: José compró 3/4 de un pastel y su hermana María comió 2/8 del mismo pastel. ¿Cuánta cantidad del pastel queda sin comer?
- Problema 2: En un partido de baloncesto, los hermanos Lucas y Pedro anotaron 2/5 y 3/10 canastas respectivamente. ¿Cuántas canastas anotaron en total?
Aplicaciones geométricas de las fracciones
Las fracciones tienen aplicaciones muy interesantes en el ámbito de la geometría. A continuación, se presentan algunas de las principales aplicaciones geométricas de las fracciones:
- División de segmentos: Las fracciones permiten dividir un segmento en partes iguales, lo que resulta útil para determinar puntos medios o trazar divisiones proporcionales en una línea recta.
- Áreas de figuras: Las fracciones se utilizan para calcular áreas de figuras geométricas irregulares. Al dividir una figura en partes iguales, se pueden determinar las áreas de cada sección en forma de fracción.
- Porcentajes y proporciones: Las fracciones son fundamentales para comprender conceptos de porcentajes y proporciones en geometría. Al expresar una fracción como un porcentaje, es posible visualizar la relación entre partes y el todo en una figura geométrica.
- Escalas: Las fracciones se usan para representar las escalas en planos y mapas. Al relacionar las dimensiones de un objeto en el plano con las dimensiones reales, se puede emplear una fracción para indicar la proporción entre ambas.
- Coordenadas fraccionarias: Las fracciones se utilizan en el sistema de coordenadas para representar puntos que no se encuentran en posiciones enteras. Esto permite ubicar con precisión puntos intermedios en un plano cartesiano.
Estas aplicaciones geométricas demuestran la importancia y versatilidad de las fracciones en el estudio de las figuras y las medidas. Su uso en contextos geométricos facilita la resolución de problemas y la comprensión de conceptos clave en esta área de las matemáticas.
Fracciones y números decimales
En el estudio de las fracciones, es importante comprender la relación que tienen con los números decimales. Los números decimales representan cantidades que se expresan en una fracción decimal, donde el numerador es un número entero y el denominador es una potencia de 10.
Al relacionar las fracciones con los números decimales, se puede visualizar cómo se representan las partes de un todo en forma decimal. Esto es especialmente útil al realizar operaciones con fracciones, ya que se pueden convertir a su equivalente decimal para facilitar los cálculos.
- Para ello, podemos utilizar estrategias como la división para transformar la fracción en un número decimal.
- También es posible convertir un número decimal a fracción, identificando el lugar decimal y considerándolo como un denominador de 10, 100, 1000, etc.
La comprensión de la equivalencia entre fracciones y números decimales es fundamental en la resolución de problemas matemáticos y en el razonamiento lógico. Además, nos permite relacionar conceptos y fortalecer el entendimiento de la aritmética y las operaciones con fracciones.
Estas fichas de fracciones permiten asignar tareas, realizar un seguimiento del progreso de los estudiantes y proporcionar resultados autocorregidos. Esta función facilita la evaluación y el seguimiento del aprendizaje de los estudiantes de una manera más efectiva.